Writing Monads in Scala with Spark-Notebook

22 minutes read

Douglas Crockford once said that people who finally understand Monads immediately lose the capability to explain them to others. Well, the few readers of this chaotic blog are lucky: neither I understand them nor am able to explain them anyway. However, I can say in advance that a Monad in Scala is something that implements two methods: map and flatMap. Haskell coders (luckily, they’re certainly not reading this blog) now would say: No, there’s no flatMap but only bind written as >>=. Yes, I know but anyway, we’ll stick with flatMap.

And to make this article somewhat cooler we’ll use a fantastic environment for writing Scala code called the Spark Notebook written by Andy Petrella and other Gurus from Data Fellas.

The notebook for this article can be found here.

Why using a Spark-Environment?

And yes, I can hear you asking: why on Earth are you using a Spark Notebook while explaining monads in Scala? Spark is a parallel execution environment, suitable for complex computational tasks, utilizing Hadoop, YARN, Mesos, offering  packages like Streaming, GraphX, SparkSQL, MLlib etc.

Well, the reason is simple: I like to write my Python codes with Jupyter (The Artist Formerly Known As IPython) and the Spark Notebook brings everything I know and love from it. Spark-Notebook itself is based on an older project called Scala-Notebook. I’ve also used Scala Notebook to write some Scala but from my perspective working with it isn’t as slick and easy as it’s with Spark-Notebook. Therefore, regardless if you’re working “for real” with Spark or just wanting to write your Scala code via a WebBrowser, I strongly recommend to give Spark-Notebook a chance. One additional reason is that you can directly download a pre-configured package optimized for your individual Spark/Hadoop/Scala Version. If there’s no pre-packaged environment directly available you can always let spark-notebook.io generate one for you.

I, for example, use Scala v.2.12.0-M3, Spark 1.5.1 and Hadoop 2.6.0. If you’re a Windows user like me you’d surely like to avoid building Hadoop and rather download a pre-packaged version. If this is the case then I’d recommend to go here and download a precompiled version 2.6.0. I’ve also written a small article on using Scala and Apache Spark.

Starting Spark-Notebook

After you’ve collected all the needed packages, unpack them and go to your console and start Spark Notebook by executing the bin/spark-notebook Script. You’d see an output similar to this one:

Our Spark-Notebook is now ready and waiting for commands via Browser on port 9000!  😀

Now, all of you who already know how to work with Jupyter will have no problems to orient yourselves within Spark-Notebook. Just click on “New” and create a Notebook based on Scala and your Spark environment:

What is a Monad?

Well, it’s really, really better to avoid any definitions especially if you’re not able to precisely describe a Thing™. And because a Monad is a Thing of Things™ I don’t want to pretend to be a experienced functional programmer. Therefore, I’ll apply a strategy I call: look and say. As you may already know by reading these sentences, English is not my native language and the semantics often feel coarse and not very colorful. This happens when you (mis)use “living things”, like natural languages, only to solve some technological tasks, which are mostly based on maths/logic and the like. I’m almost exclusively using English to talk and read about things related to technology and usually don’t need to inject much “life blood” into my sentences. It’s like writing COBOL with a bit more modern syntax. 😆 To me learning English never was a learning process by itself because I never saw it as an “natural language” for communicating with people. Yes, I know, we coders are humans too and I really don’t want to talk about silly stuff like “Programmers are organisms that turn coffee and pizza into code“…that’s stupid and I’m simply too old for such silly jokes.

It’s like wanting to reduce complexity to something we can control and use without fearing the side-effects. And the same I did while unconsciously learning the English language. I never let the English language be more than a vehicle for bringing me from a technical problem A to a solution B. This is, for example, the reason why I’ve never learned to properly distinguish between Present Perfect Simple and Simple Past and other things I can’t even name properly.

Ok, I know, you’re presumably asking yourself why I’m talking about. Well, monads are all about reducing complexity. Now let me explain why I want you to learn monads by: look and say.

On Spelling of English and Monadic structures

As we all know the spelling of English is a perfect example when side-effects slip into a language. Of course, I’m not saying that this only happened to English as all natural languages evolve over time but English is a very good example on what can happen when multiple languages heavily influence some other language at the same time. The extraordinary history of United Kingdom (and its predecessors) created a language that now shows traits of many different languages. In many English sentences you can see traits from Norse, French and Old Germanic. Often in the same sentence! Of course, such heritage developed a complex set of spelling rules leaving non-native speakers only one “successful” strategy to learn the language: learn the words by heart. Avoid learning the spelling rules as long as you can, so you may avoid their complexities as well. I can’t know the educational system in the English-speaking countries but I’ve read about one of the methods called: look and say . So, the kids just learn to recognize “word blocks” and repeatedly read them out loud until they have learned them by heart. In fact, they don’t learn to see the words as “combined letters” but rather as patterns or blocks, as I would say from my non-English perspective. I may be totally wrong and this article is really not about education. This small digression served me as an example on how complexities can be reduced to something very simple yet powerful: look and say! And this will be my apparatus for describing Monads in Scala. I hope you now accept why I didn’t want to pretend to know anything about some “precise scientific/mathematical/whatever” definitions of Monads. They’re too complex to explain without showing them as they are in the first place. I’m not saying that learning a for-each-loop, for example, is possible without showing it first. But, a for-each-loop has at least some connection to unrelated loops in the real world. At least you can imagine a loop before learning for-each-loops. Sadly, Monads are like Yetis. We have to see them first!  😯

Look at it and say: it is a Monad!

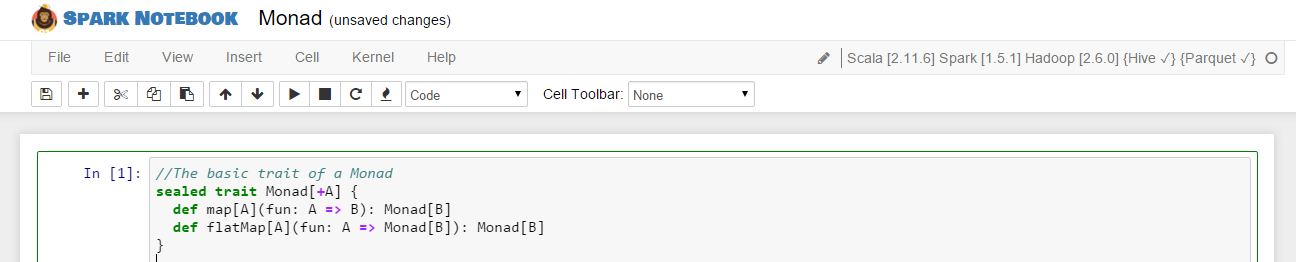
By using Scala-oriented terms the most simple definition of a monad is: A Monad is a thing comprising of two methods map and flatMap. So, first we should ignore the definitions of map and flatMap and just learn the most basic structure of a Monad written in Scala’s terms. We now open a new notebook and write a new Trait:

We see that our Monad trait prescribes a thing of a certain Type (+A, which is btw. a covariant type) that can produce new Monads of some other type (B) by using its map and flatMap methods. And how does this thing produce new Monads? The trait describes its two methods as methods who expect to be fed with some external functions provided as arguments. If we look into the signature of map and flatMap we’d see that they expect their callers to provide them functions of certain types. map expects a function of type A => B while flatMap expects A => Monad[B]. This means that map and flatMap only accept functions with certain signatures.

This means that before we can successfully call map and/or flatMap we have to have two functions like these:

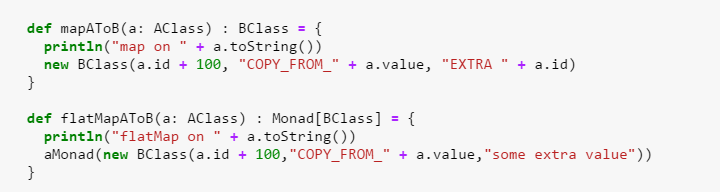
Here we define mapAtoB and flatMapAtoB as functions doing the following:

• mapAtoB takes an instance of type AClass and returns an instance of BClass (we say: it maps A to B)
• flatMapAtoB takes an instance of type AClass and returns an instance of type Monad[B] that contains an instance of BClass

The println calls are only for additional logging in the console.

Before going deeper the first thing we have to learn is that by looking at these two methods we can say that a Monad is a container type. An instance of a Monad contains some things (instances of classes, for example) and does something with them or to them. Here we can clearly see that our Monad takes some externally defined functions and uses it to do something to things it contains. As a result our Monad either creates new instances of some other class or instances packed into a new Monad. If we look at the definition of our trait we see that it’s defined as Monad[+A] but the returned types from map & flatMap are of type B respective Monad[B]. These return types are “other classes” I mentioned previously. So, a Monad is capable of returning new types. Therefore, we can also say that a Monad is also a type constructor. Monads not only can contain an instance of a certain types but are also capable of constructing other instances based on some class definitions. The root of this capability lies in the function map.

A Monad is a Functor

Actually, I don’t want to annoy you with any mathematical terms but some of them can’t be easily translated into normal words like the term Functor. The most simple definition of a Functor I could give is that a Functor is a Mapper between types.  When you define a Functor you give it a function to map from some things to some other things. Therefore, we can recognize Functors as factories because they help us to create new instances of some types. Previously we’ve defined a map method for our Monad and this was basically the moment we declared our Monad to be a Functor! Additionally, we also have to recognize map-methods as transformer-methods. I suppose that many Scala users see map as a better alternative to for-loops and rightfully use it as a declarative replacement of the for-loop.

Of course, there’s almost no reason not to use map instead of for. But when dealing with Monads you should, please, take into account that map inside a Monad is not a logic to “iterate over things” but to “transform the things“. If you look at the signature of the function you have to provide to map you see that it returns a different type (A => B) and the final result of map is a new Monad[B]. So, the things enter your map as instances of A but leave them as instances of B (packed in a Monad, of course). Therefore, again: map is a transformer!

A simple Monad in the wild

Because we already know that a Monad is a container of things we can now imagine it would contain a List of Integers. This means that the concrete type of our Monad[+A] instance is now Monad[List[Int]]. First, we create a case class aMonad (silly naming, yes, I know) that extends our trait Monad[+A] so we can use it to create a instances of Monads specialized to contain Lists of Integers:

We use case classes as factories to instantiate our Monads:

Also we have to take into account the special case when there’s no value. Later we’ll see why we need such Monads.

This is it! Our numMonad is now a Monad containing a List of Integers. And because it extends the trait Monad[+A] it already contains the needed declarations to do map and flatMap operations.

We’ve already defined mapAtoB we let our Monad use them to do something to the list it contains inside. In this case a map means nothing else but: go over the elements of the list you contain and execute on each of them the function I gave you. So, the final result of this operation is a new list containing elements of a different type (in our case: List of Strings) but it retains the shape of the original list. This means, for example, that if the original list contained 100 Integers the resulting list would contain 100 Strings. THIS is what makes Monads and operations with them composable and side-effect free. No matter what happens inside (even if types completely change) the look from from the outside would remain the same. We only once recognize a Monad. There’s no need to put a silly amount of try-catch or if-then-else-statements just to be sure that it isn’t going to blow up the rest of your code if something inside of it changes. It’s exactly the opposite: with Monads the elements may change (like their types, values, whatever), but the shape will remain the same. And as long as the shape of a (probably interconnected) thing doesn’t change there will be no side-effects and it would never wreak havoc on some other parts of the program.

And what does flatMap do?

First, we have to recognize the kind of the provided function argument. Unlike map that uses just a “normal” function to apply it to each of the elements flatMap uses a monadic function. This means that the result of a flatMap call is a new Monad.

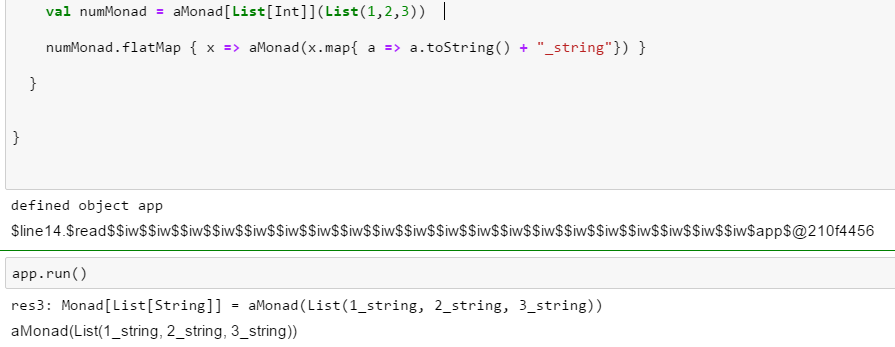
Here we see how it looks like in our example:

We take each of the elements from the original List[Int] and create a new Monad of type List[String] that contains all the Strings we’ve created by converting the original Integers, one by one. It may be somewhat hard to recognize it immediately but a flatMap simply generates a new Monad by executing the function we provided as the argument. A flatMap promises to return a Monad that will contain something of the same shape like the structure in the original Monad but this new shape will be generated by a function located inside the constructor of the new Monad. Here the new Monad constructs itself by using our function, so to speak. In map there’s no construction of a new Monad but just changing the elements of the current one. Here we should remember that a Monad is also a type constructor and not only an element container.  When we use map we touch the container-nature of a Monad. When we execute flatMap we touch it’s type constructor-nature.

Here’s what happens with our Monad:

We define a new Monad by using the already known case class aMonad. This Monad contains a List with three Integers. We feed it’s flatMap with a function that creates a new Monad by using the same case class but this Monad’s constructor receives the result of the execution of the “embedded” map call over each of the elements of the “outer” Monad that owns the original List[Int].

The inner logic of map and flatMap

We have learned what the functions provided as arguments do inside our Monads. Now let’s see the nature of map and flatMap in the respective Monad class definitions.

Inside the trait Monad[+A] are the default definitions of map and flatMap. The two case classes extending it don’t define or override any additional methods. Of course, this would possible and there’s nothing preventing you from defining your own overrides or adding any new methods. A Monad is still an object. Now, there’s a special Monad extending from trait Monad[Nothing] which serves a very important role: it protects us from those pesky NullPointerReference exceptions. As we know, a Monad is also a type container and some of those types are allowed to be “null”. Dealing with such variables always leads to heavy try-catch and/or if-then-else blocks. Also, there are many situations where you simply can’t be careful enough to catch all possible Null-Pointer-Values. Just think of any shared memory stuff or any kind of parallelisms, multi-threading etc. In such cases having a Monad taking care of values and their manipulations is an advantage. In our simple case the Monad uses pattern matching to check if the current value inside a Monad is of a certain type. This is the reason why we are using case classes. They provide us the powerful pattern matching feature of Scala. As we saw earlier in the definition of our NullMonad its default type is Nothing which is a subtype of any other type in Scala (including scala.Null). This means that we can use Monad[Nothing] to guard ourselves from NullPointerExceptions no matter what kind of class we might define in future. We can always be sure that our Monad[Nothing] will remain capable of catching all “invalid” values. We now understand why pattern matching in map and flatMap was used: both could potentially receive a Null leading to some undefined behaviors or results. This, of course, is by no means the only reason why you should use pattern matching. For example the so-called “optional values”, better known as Maybe from Haskell, can be easily implemented by using similar constructs. I’ve created a small example and put it above our Monad’s definition. Interested readers may try to play for a bit with this Option[A] monad.

Alternative way to define a flatMap

When it comes to define flatMap and use map then there’s more than one way to do it. A flatMap is, as it’s name suggests, a method that flattens a list of things. Or more technically: a flatMap ultimately executes the map-method. No matter how the elements entered flatMap, all of them will end up being iterated over by map which transforms them as we’ve already learned. Or even simpler defined: using a flatMap on an element (or elements) generates a new collection for each of those elements.  But at the end of the flatMap-operation all of those lists will be combined into one final collection (that is, it “flattens” the collections). A flatMap could generate multiple Iterables but in the end it will use their Iterators to pack all of the elements into the final collection which is then returned inside a Monad.

Therefore we can also define flatMap as a method that takes a List of Monads of some type and forwards them to the inner toFlatList-method. The name toFlatList is not mandatory. toFlatList receives the result of the map-call because map is always the last method executed by flatMap. By invoking map we use the aforementioned Iterators, of course. Inside toFlatList we check the Monad type returned by the inner map and act accordingly.

Monads are good for controlling side-effects and managing state

To convince you that Monads are of advantage when it comes to managing state and dealing with side-effects I’ve created a small example that assembles Robots and converts them without disrupting the external state of the app.

We first define a simple trait called Robot. Based on it we define C3PO and Data classes. Later we’ll define some C3PO’s and convert them to Data’s. And because they’ll be guarded by Monads no matter what we do with them (or to them) everything will remain inside the Monadic Armor™.

Robot case classes with their respective overrides (name & model properties).

This is just to have something to be written to the console (we need some side effects!)

After having defined the needed overrides, because we want our robots speak for themselves, we create a Monad of type List[C3PO] and test each of them by calling its say–method (imagine, we produce robots and want to test them before letting them go out).

Now we want our C3PO’s to be upgraded to Data’s but without touching them directly or dealing with any kind of internal state. This is ugly and not very composable. As we already know, with a little help from Monads we can easily combine different parts of our programs as long as their shape doesn’t change or dictate the shape of the environment. We know that Monads support higher-order functions because we already called map and flatMap while providing them functions with a certain signature as arguments. We can now create a new that takes a Robot and based on some internally defined logic reassembles it into another one.

Our side-effect-producing logic is located in only one place and is effectively invisible to the outer world. What’s visible is: a Robot goes in and a Robot goes out. But that’s not everything. We have to put this logic into the Monadic Armor™.

Now we have a proper transformation! As we’ve already defined, a map is not a loop in disguise but a transformation. Here we can see it in action. Each Robot, called nextRobot, from the allRobots-List goes into map which calls upgradeRobot that returns a new robot. This new Robot is then put into a Monad.

A quick test shows us that all of the robots have been properly reassembled.

Why and when should we use Monads?

Well, this is actually a mine field because there are so many discussions around that I’d rather avoid putting my “opinion” in the round. I’m also not very experienced with Monads and functional programming in general, so it’s better for me to stay away from any discussion. I can only speak for myself: I’d rather prefer to have small, composable and mostly side-effect-free structures, if possible. This means, whenever I have to deal with stuff that changes my data and could (or will!) sooner or later provoke some unexpected effects. The advantage is that dangerous parts are effectively “taken into custody”  and I can later easily (re)compose my Monads in different ways.

Conclusion

I hope that these few examples were sufficient enough to convince you to use Monads and Spark-Notebook. Monads are perfect armors to guard you from side-effects and complexities which are practically unavoidable because we want our software to be usable. And usable software means software interacting with our world that is full of side-effects, entropy and complexity. However, using the software in the real world doesn’t mean to accept the complexity and state as something “unavoidable” but rather as one of the many aspects we, software developers, have to deal with. And just like we use certain programming languages to solve certain types of tasks the same should apply to Monads and functional programming.

Regarding Spark-Notebook I can only say:

Use it because it’s:

• easy to configure,
• helping you to configure your preferred environment,
• web-based,
• open source

These days no software can call itself “modern” without being directly connected to the web. Backends may be perfectly configured but the real work comes from the opposite direction.